파이토치 위키독스 공부하기
05-01 One-Hot Encoding
1.One-Hot encoding
- 원-핫 인코딩=선택애야하는 선택지 개수만큼의 차원을 가진다.
각 선택지의 인덱스에 해당하는 원소는1의 값, 나머지는 0의 값을 가지는 표현 방법
- 원-핫 벡터=원-핫 인코딩으로 표현된 벡터
ex)
강아지 0번 인덱스, 고양이 1번 인덱스, 냉장고 2번 인덱스 이다.
선택지에 대해서 원-핫 인코딩 된 벡터는 다음과 같다
강아지=[1,0,0] 고양이=[0,1,0] 냉장고=[0,0,1]
위의 벡터들은 원-핫 벡터
2. 원-핫 벡터의 무작위성
대부분의 '다중 클래스 분류 문제'는 클래스 간의 관계가 균등하므로
원-핫 벡터로 표현하는것이 적절하다
그런데 이때 정수 인코딩을 사용할수 있지 않을가 생각을 할 수 있다.
예를들어 Banana, Tomato, Apple 3개의 클래스가 존재하는 문제가 있다.
정수 인코딩으로 1,2,3을 부여했다.
이 경우에 MSE(평균 제곱 오차)를 적용해보자
실제값이 Tomato일때 예측값이 Banana이면 제곱 오차는 (2-1)^2이다.
실제값이 Apple일 때 예측값이 Banana이면 제곱 오차는 (3-1)^2이다.
Banana,Tomato사이 오차보다 Banana,Apple 사이의 오차가 더 큰것이다.
이는 Banana가 Apple보다 Tomato에 가깝다는 정보인데
이 경우에 이런 정보는 의도하지 않은 정보이다(일반적인 분류 문제에서는 클래스 순서가 의미를 가지지 않는다)
이처럼 순서가 중요하지 않을때는 클래스 간의 오차는 균등해야한다.
따라서 원-핫 인코딩 방식을 사용하는 것이고,
원-핫 인코딩을 통해 레이블을 인코딩했을 때 클래스간의 제곱 오차는 균등하다
((1,0,0),(0,1,0)^2)=2
((1,0,0)-(0,0,1))^2=2
다르게 말하자면
모든 클래스에 대해서 원-핫 인코딩을 통해 얻은 원-핫 벡터들은
모든 쌍에 대해서 유클리드 거리가 동일하다.
원 핫 벡터는 이처럼 각 클래스 표현 방법이 무작위성을 가진다는 것이다.
이런 무작위성은 때로는 단어의 유사성을 알 수 없다는 단점으로 언급되기도 한다.
05-02 소프트맥스 회귀 이해
소프트맥스 회귀로 3가지 이상 선택지 중에 1개를 고르는 다중 클래스 분류를 실습해보자
1. 다중 클래스 분류(Multi-class Classification)
다중 클래스 분류 = 3가지 이상의 선택지 중에 하나를 고르는 것
붓꽃 품종 분류하기 = 유명하고 전형적인 다중 클래스 분류 문제이다
꽃받침 길이, 꽃받침 넓이, 꽃잎 길이, 꽃잎 넓이라는 4개의 특성으로 부터
3개의 붓꽃 품종중 어떤 품종인지 예측하는 문제이다
X=입력
W=가중치
B=편향
Y^=출력(예측값. H(X))
- 로지스틱 회귀
시그모이드 함수로 예측값을 0~1사이로 나오게 한다.
출력이 0.75라면 Class1일 확률이 75%, Class2일 확률이 25%라는것.
(두 확률의 총 합은 1)
H(X)=sigmoid(WX+B)
- 소프트맥스 회귀
위의 아이디어를 다중 클래스 분류 문제에 적용.
각 클래스(선택지) 마다 소수 확률을 할당한다.
각 선택지가 정답일 확률을 나타내는것.
총 확률 합은 1이다.
H(X)=softmax(WX+B)
2.소프트맥스 함수
=여러 클래스에 대한 확률을 추정한다.
소프트맥스 함수
zi=k차원 벡터에서 i번째 원소
pi=i번째 클래스가 정답일 확률
소프트맥스 함수

p1=1번 클래스가 정답일 확률
p2=2번 클래스가 정답일 확률
...
pn=n번 클래스가 정답일 확률
각각의 확률은 0과 1사이의 값이며 총 합은 1이다.
붓꽃 분류 문제에서 3개의 클래스는 virginica, setosa, versicolor이다.
p1=입력이 virginica일 확률
p2=입력이 setosa일 확률
p3= 입력이 versicolor일 확률
이다.(순서는 안중요하다) 식을 문제에 맞게 쓰면 아래와 같다.

이제 더 깊이 공부해보자
1). 소프트맥스 함수의 입력 벡터
=붓꽃 분류 데이터는 4개의 독립 변수 x를 가진다.
모델에 4차원 벡터를 입력으로 넣고 싶다는 말이다.
하지만 소프트맥스 함수는 '분류하고자 하는 클래스 개수' 크기의 벡터를 입력 받는다.
(붓꽃 데이터에서는 클래스가 3개이므로 3차원 벡터를 입력 받아야한다.)
따라서 입력은 가중치 연산을 통해 4차원에서 3차원 벡터로 변환되어야 한다.
차원을 어떻게 축소할까? 가중치 곱을 진행하면 된다.
- z벡터= 소프트맥스 함수의 입력 벡터
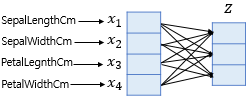
x1,x2,x3,x4는 다 다른 가중치를 가진다.
학습을 통해서 오차를 최소화하는 가중치로 값이 변경될 것이다.
이제 z벡터의 차원수만큼 가중치 곱을 진행하면 된다.
2) 오차 계산 방법
소프트맥스 함수의 출력은 '분류하고자 하는 클래스 개수' 크기의 벡터이며
원소들은 0과 1사이의 값을 가진다.
이 각각의 값들은 특정 클래스가 정답일 확률이다.
(여기서 p1=virginica가 정답일 확률, p2=setosa가 정답일 확률, p3=versicolor이 정답일 확률)
예측값과 비교할 수 있는 실제값의 표현방법이 필요한데
소프트맥스 회귀에서는 실제값을 아래와 같이 원-핫 벡터로 표현한다.

예를 들어 샘플 데이터 실제값이 setosa라면 setosa의 원-핫 벡터는 [0 1 0]이다.
이 때 소프트맥스 함수 결과가[0 1 0] 라면 예측값과 실제값의 오차가 0일 것이다.
예측값이 [0.26, 0.71,0.04]으로 나왔다고 하면 실제값[0 1 0]과 비교해
그 오차로 w(weight), b(bias)를 업데이트한다.
(오차를 계산하기 위해서 비용 함수로 크로스 엔트로피 함수를 사용하는데 나중에 설명할 것이다)
소프트맥스 회귀를 벡터와 행렬 연산으로 이해해보자.
소프트맥스 회귀에서 예측값을 구하는 과정은 다음과 같다.
x=입력 벡터, W=가중치 행렬, b=bias, f=특성의 수, c=클래스 개수

3. '붓꽃 품종 분류' 행렬 연산으로 이해하기

입력 행렬 X
=예제의 데이터 전체 샘플 개수는 5개, 특성 4개이므로 5x4크기이다.
편의를 위해 각 행렬의 원소 위치를 반영한 변수로 표현했다.


예측값 행렬 Y
=선택지가 3개 이므로 열 개수는 3개이다.
각 행은 행렬 X의 각 행 예측값이므로 동일해야 한다.
결과적으로 5x3이다
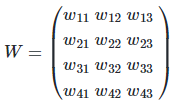
가중치 행렬 W
= (예측값 행렬Y=입력 행렬X x 가중치 행렬W) 이므로
추정을 통해 가중치 행렬은 4x3임을 알 수 있다.

편향 행렬 B
=예측값 행렬Y와 크기 동일하므로 5x3
결과적으로 가설식은
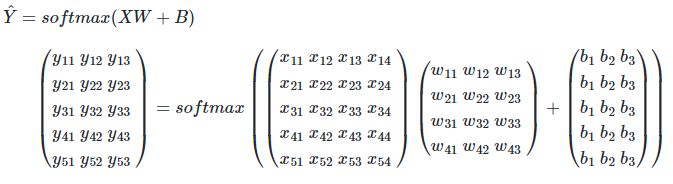
4. 비용함수(cost function)
소프트맥스 회귀에서는 비용함수로 크로스 엔트로피 함수 사용한다.
1) 크로스 엔트로피 함수
y=실제값, k=클래스 개수
yj=실제값 원-핫 벡터의 j번째 인덱스
pj=샘플 데이터가 j번째 클래스일 확률 (
y^j로 표기하기도 한다)

이 함수가 왜 비용함수로 적합할까?
숫자 c가 실제값 원-핫 벡터에서 1을 가진 원소의 인덱스라고 하자.
그러면 Pc=1은 정확하게 예측한 경우이다.
이것을 식에 대입해보면 log(1)로 크로스 엔트로피 함수 값은 0이다.
즉 이 함수 값을 최소화 하는 방향으로 학습하면 된다.
이를 전체 데이터에 대한 평균을 구해보면 최종 비용함수는 다음과 같다

2) 이진 분류에서 크로스 엔트로피 함수
아래는 로지스틱 회귀에서 배운 크로스 엔트로피 함수식이다

위의 식에서 y --> y1, 1-y --> y2, H(X)--> p1, 1-H(X)--> p2로 치환해보자
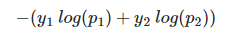
위의 식은 다음과 같이 표현할 수 있다
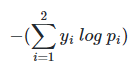
소프트맥스 회귀에서 k값은 고정된 값이 아니므로 2를 k로 변경한다
이제 소프트맥스 회귀식을 구했다!
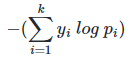
+) 결과적으로 소프트맥스 함수의 최종 비용함수에서 k가 2라고 가정하면 결국 로지스틱 회귀의 비용함수와 같다.
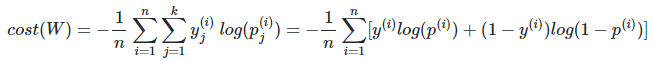
'개발 > AI' 카테고리의 다른 글
| [OpenCV] 컴퓨터 비전과 딥러닝 / Ch04 / 연습 문제 (1) | 2024.08.03 |
|---|---|
| [Pytorch] 06. 인공 신경망 (2) | 2024.08.02 |
| [Pytorch] 04. 로지스틱 회귀 (0) | 2024.07.30 |
| [PyTorch] 03. ML 입문 하기 (0) | 2024.07.29 |
| [OpenCV] 컴퓨터 비전과 딥러닝 / Ch03 / 연습 문제 (0) | 2024.07.08 |



