파이토치 위키독스 공부하기
03-01 선형회귀
1. 데이터에 대한 이해
훈련 데이터셋=예측을 위해 ML학습시키기 위한 데이터
테스트 데이터셋=모델이 작동을 잘하는지 판별하기 위한 데이터셋
훈련 데이터셋 구성
입력 X, 출력 Y
2. 가설 수립
머신러닝에서 세우는 식.
ex) 선형회귀 가설(직선의 방정식)
y=Wx+b
H(x)=Wx+b
W=가중치, b=편향(bias)
3. 비용함수
비용함수(cost function)=손실함수(loss function)=오차함수(error function)=목적함수(objective function)
랜덤으로 W, b의 값을 설정했을 때 목표점들을 가장 잘 지나가는 직선을 구하고자 한다.
이때 직선이 점들을 얼마나 잘 나타내는지 판단하는 기준으로 "오차"를 사용한다.
오차=실제값(y^i)-예측값(H(x^i))

오차값이 음수일 때도 있으므로 제곱 합의 평균으로 "비용함수"를 정의한다.
4. 옵티마이저-경사 하강법(Gradient Descent)
비용함수를 최소로 하는 W, b값을 찾고자 할 때 옵티마이저 알고리즘을 사용한다.
training=옵티마이저 알고리즘을 통해 적절한 W, b를 찾아내는 과정
Gradient Descent=가장 기본적인 옵티마이저 알고리즘
y=Wx(b=0이라고 가정)에서 W를 생각해 보자. W가 너무 커지거나 너무 작아지면 오차가 커진다.
(b 또한 마찬가지) 따라서 W와 비용함숫값의 관계는

다음과 같다.
따라서 가장 최적의 함수를 찾기 위해서는
cost(비용함수) 값이 가장 작은 W를 찾아야 한다.
W 초기값을 주고 맨 아래 볼록한 부분을 향해 W를 수정해 나간다. 이것이 Gradien DEscent이다.
w에 해당하는 접선의 기울기가 0에 근접해질 때까지 한다.
이 작업은 W에 접선의 기울기를 구해 특정 숫자 알파를 곱한 값을 빼서 새로운 W로 사용하는 식이 사용된다.

- 기울기가 음수일 때 --> W값이 증가한다.

- 기울기가 양수일 때 --> W값이 간소한다.

즉 아래의 수식은 접선의 기울기가 양수, 음수인 경우 둘 다 0인 방향으로 W값을 조정한다.

알파=학습률. W값을 얼마나 크게 변경할지 결정.
알파값이 너무 크다면 cost값이 발산하고 알파값이 너무 작으면 시간이 너무 오래 걸리므로 적당한 값을 찾는 것이 중요
이처럼 경사 하강법은 최적의 w, b를 찾아간다.(이 경우에서는 b는 생각 안 했지만)
5. 파이토치로 선형 회귀 구현
#basic setting
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)#-->난수 발생시 값 동일하게 보장시켜준다. 항상 같은 결과 나오게 된다
x_train=torch.FloatTensor([[1],[2],[3]])
y_train=torch.FloatTensor([[2],[4],[6]])
#Initiate w,b to 0(weight, Bias)
W=torch.zeros(1,requires_grad=True)
b=torch.zeros(1,requires_grad=True)
#SGD(gradient descent)
optimizer=optim.SGD([W,b],lr=0.01) #lr=learning rate
nb_epochs = 1999 # gradient descent를 반복하고 싶은 횟수
for epoch in range(nb_epochs + 1):
# H(x) 계산. 가설세우기
hypothesis = x_train * W + b
# cost function
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()#set gradient 0 -->파이토치는 미분을 통해 얻은 기울기를 이전에 계싼된 기울기 값에 누적시키는 특징이 있기 때문에 초기화시켜줘야한다.
cost.backward()#calculate gradient
optimizer.step()#update W,b
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), b.item(), cost.item()
))
03-02 자동미분
경사 하강법을 직접 코딩하는 것은 까다로우므로 파이토치에서 자동 미분(Autograd)을 지원한다.
import torch
#임의의 w값(2)
w=torch.tensor(2.0,requires_grad=True)
#수식정의
y=w**2
z=2*y+5
#기울기 계산
z.backward()
print('수식을 w로 미분한 값:{}'.format(w.grad))
03-03 다중 선형 회귀
1. 변수 3개 데이터
3개의 값(특성)으로 최종 점수를 예측하는 모델을 만들어보자.
독립변수 x가 3개라서
H(x)=w1x1+w2x2+w3x3+b
라는 수식을 구할 수 있다.
파이토치로 구현
#3-3
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
# 훈련 데이터
x1_train = torch.FloatTensor([[73], [93], [89], [96], [73]])
x2_train = torch.FloatTensor([[80], [88], [91], [98], [66]])
x3_train = torch.FloatTensor([[75], [93], [90], [100], [70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
# Initiate weight, bias
w1 = torch.zeros(1, requires_grad=True)
w2 = torch.zeros(1, requires_grad=True)
w3 = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
#set optimizer
optimizer=optim.SGD([w1,w2,w3,b],lr=1e-5)
nb_epochs=1000
for epoch in range(nb_epochs+1):
#H(x)
hypothesis=x1_train*w1+x2_train*w2+x3_train*w3+b
#cost
cost=torch.mean((hypothesis-y_train)**2)
#calculate H(X)
optimizer.zero_grad()
cost.backward()
optimizer.step()
#print log
if epoch % 100 == 0:
print('Epoch {:4d}/{} w1: {:.3f} w2: {:.3f} w3: {:.3f} b: {:.3f} Cost: {:.6f}'
.format(epoch, nb_epochs, w1.item(), w2.item(), w3.item(), b.item(), cost.item()))
2. 벡터와 행렬 연산으로 바꾸기
위의 코드를 개선하는 법을 알아보자
x1_train, x2_train,... w1, w2... 등으로 하나씩 변수를 선언했는데 이와 같은 방법은 비효율적이다.
이를 해결하기 위해 행렬곱셈 연산을 사용할 수 있다
이를 위해 가설을 벡터와 행렬 연산으로 표현해 보자

다음과 같이 내적으로 표현할 수 있다.

위의 벡터를 X, W로 표현한다면
H(X)=XW로 간단하게 수식이 바뀐다.
이를 활용해서 파이토치로 구현해 보자
import torch
x_train=torch.FloatTensor([[73,80,75],[93,88,93],[89,91,80],[96,98,100],[73,66,70]])
y_train=torch.FloatTensor([[152],[185],[180],[196],[142]])
#weight and bias
W=torch.zeros((3,1),requires_grad=True)
b=torch.zeros(1,requires_grad=True)
# optimizer
optimizer = optim.SGD([W, b], lr=1e-5)
nb_epochs = 20
for epoch in range(nb_epochs + 1):
# H(x) 계산. 행렬곱으로 가설 설정
# 편향 b는 브로드 캐스팅되어 각 샘플에 더해집니다.
hypothesis = x_train.matmul(W) + b
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
print('Epoch {:4d}/{} hypothesis: {} Cost: {:.6f}'.format(
epoch, nb_epochs, hypothesis.squeeze().detach(), cost.item()
))
03-04 nn.MOudle로 구현하는 선형회귀
1. 단순 선형회귀 구현
비용함수를 직접 정의하지 않고
파이토치에서 이미 구현되어 제공되는 함수를 불러와서 모델을 구현해 보자
nn.Linear() = 선형회귀 모델
nn.functional.mse_loss()=평균제곱오차
단순 선형회귀 구현하기
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(1)
x_train=torch.FloatTensor([[1],[2],[3]])
y_train=torch.FloatTensor([[2],[4],[6]])
model=nn.Linear(1,1)#하나의 입력 x에 대해 하나의 출려y를 가진다
print(list(model.parameters()))#model에는 W,b값이 저장되어 있다. 랜덤 초기화되어있다. 첫번쨰가 W 두번쨰가 b
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)
#gradient descent repeat 2000
nb_epochs = 2000
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수
# cost로 H(x) 개선
optimizer.zero_grad()# gradient를 0으로 초기화
cost.backward() # cost function 미분하여 gradient 계산
optimizer.step()# W, b 업데이트
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(epoch, nb_epochs, cost.item()))
위의 학습 결과를 확인해 보자
#학습 결과 확인
input_var=torch.FloatTensor([[4.0]])
#입력값 4에 대한 예측값을 저장. forward연산
pred_y=model(input_var)
print(pred_y)
#학습 완료 후 W,b출력
print(list(model.parameters()))입력 4에 대한 출력은 8에 가깝게 되었으며
W=2, b=0에 가깝게 되었다
2. 다중 선형 회귀 구현
다중 선형회귀를 구현해 보자. nn.Linear()의 인자값과 학습률만 조정해 주면 된다
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(1)
# data
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
model=nn.Linear(3,1)#3개의 x로 하나의 y를 예측
optimizer=torch.optim.SGD(model.parameters(),lr=1e-5)
nb_epochs = 2000
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)# model(x_train)은 model.forward(x_train)와 동일.
# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수
# cost로 H(x) 갱신
optimizer.zero_grad()# gradient를 0으로 초기화
cost.backward()# 비용 함수를 미분하여 gradient 계산
optimizer.step()# W와 b를 업데이트
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(epoch, nb_epochs, cost.item()))학습 결과를 확인해 보자
input_var=torch.FloatTensor([[73,80,75]])
pred_y=model(input_var)
print(pred_y)
print(list(model.parameters()))y값 정답은 152인데 151이 나왔다. 최적값을 찾았다.
w=0.98, 0.45, 0.58, b=0.28이 나왔다.
03-05 클래스로 파이토치 모델 구현
오직 클래스로 모델을 구현해 보자
1. 모델을 클래스로 구현
forward 연산=H(x)식에 입력 x값으로부터 y를 얻는 것
#단순선형회귀모델 구현
class LinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear=nn.Linear(1,1)
def forward(self,x):
return self.linear(x)
model = LinearRegressionModel()
#다중 선형회귀모델 구현
class MultivariateLinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear=nn.Linear(3,1)
def forward(self,x):
return self.linear(x)
model = MultivariateLinearRegressionModel()
model을 설정하여 사용하면 된다.
03-06 미니 배치와 데이터로드
1. Mini Batch & Batch Size
Mini Batch=데이터가 수십만 개 이상이면 전체 데이터에 경사하강법을 수행할 시 너무 느리고 많은 계산양을 요구할 것이다. 그렇기에 전체 데이터를 작은 단위로 나눠서 단위별로 학습하는 개념이 있다
이때 이 단위를 Mini Batch라고 한다.
batch size=미니배치의 크기
배치 경사 하강법=전체 데이터 한 번에 경사하강법 수행. 가중치값이 안정적으로 최적값에 수렴하지만 계산량이 너무 많이 든다
미니 배치 경사 하강법=미니 배치 단위로 경사 하강법 수행. 최적값 얻는 것이 조금 불안정하지만 속도가 빠르다
2. Iteration
이터레이션=한 번의 epoch안에서 이루어지는 W, b update횟수
+) Epoch=전체 훈련 데이터가 학습에 한 번 사용된 주기
3. 데이터 로드하기
데이터 쉽게 다룰 수 있게 파이토치에서 제공하는 도구
TensorDataset=텐서를 입력받아 Dataset형태로 바꿔주는 함수
#3-6 data load
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
dataset = TensorDataset(x_train, y_train)#입력받은 data를 TensorDataset입력으로 사용하고 dataset으로 저장
#dataLoader --> 데이터셋, 미니배치의 크기, shuffle(epoch마다 데이터셋 섞는다)
dataloader = DataLoader(dataset, batch_size=2, shuffle=True)
#model, optimizer
model = nn.Linear(3,1)
optimizer = torch.optim.SGD(model.parameters(), lr=1e-5)
#training
nb_epochs = 200
for epoch in range(nb_epochs + 1):
for batch_idx, samples in enumerate(dataloader):
x_train, y_train = samples
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train)
# cost로 H(x) 계산
optimizer.zero_grad()
cost.backward()
optimizer.step()
if(epoch%100==0):
print('Epoch {:4d}/{} Batch {}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, batch_idx+1, len(dataloader),cost.item()))학습 확인
input_var = torch.FloatTensor([[73, 80, 75]])
pred_y = model(input_var)
print("훈련 후 입력이 73, 80, 75일 때의 예측값 :", pred_y)
03-07 커스텀 데이터셋
1. 커스텀 데이터셋
torch.utils.data.Dataset을 상속받아 직접 커스텀 데이터셋 만드는 경우도 있다.
커스텀 데이터셋 만들 때 기본적인 뼈대
class CustomDataset(torch.utils.data.Dataset):
def __init__(self):
데이터셋의 전처리를 해주는 부분
def __len__(self):
데이터셋의 길이. 즉, 총 샘플의 수를 적어주는 부분
len(dataset)이라고 하면 데이터셋 크기를 return해준다
def __getitem__(self, idx):
데이터셋에서 특정 1개의 샘플을 가져오는 함수
dataset[i]를 하면 i번째 샘플을 가져온다
커스텀 데이터셋으로 선형회귀 구현하기
import torch
import torch.nn.functional as F
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
# Dataset 상속
class CustomDataset(Dataset):
def __init__(self):
self.x_data = [[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]]
self.y_data = [[152], [185], [180], [196], [142]]
# 총 데이터의 개수
def __len__(self):
return len(self.x_data)
# 인덱스를 입력받아 그에 맵핑되는 입출력 데이터를 파이토치의 Tensor 형태로 리턴
def __getitem__(self, idx):
x = torch.FloatTensor(self.x_data[idx])
y = torch.FloatTensor(self.y_data[idx])
return x, y
dataset = CustomDataset()
dataloader = DataLoader(dataset, batch_size=2, shuffle=True)
model = torch.nn.Linear(3,1)
optimizer = torch.optim.SGD(model.parameters(), lr=1e-5)
nb_epochs = 20
for epoch in range(nb_epochs + 1):
for batch_idx, samples in enumerate(dataloader):
# print(batch_idx)
# print(samples)
x_train, y_train = samples
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train)
# cost로 H(x) 계산
optimizer.zero_grad()
cost.backward()
optimizer.step()
print('Epoch {:4d}/{} Batch {}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, batch_idx+1, len(dataloader), cost.item()))학습 확인
input_var = torch.FloatTensor([[73, 80, 75]])
pred_y = model(input_var)
print("훈련 후 입력이 73, 80, 75일 때의 예측값 :", pred_y)
03-08 벡터와 행렬 연산 복습하기
기본적인 벡터와 행렬 연산 복습해 보자
1. 벡터, 행렬, 텐서
벡터=크기와 방향 가진 양. 숫자의 나열
행렬=행과 열을 가지는 2차원 형상 rowXcolumn
텐서=3차원부터의 배열
2. 텐서
인공 신경망 모델 중 하나인 RNN에서는 3차원 텐서에 대한 개념 이해가 필수이다.
import numpy as np
#0차원 tensor(스칼라)
d=np.array(5)
print(d.ndim, d.shape)#ndim=축의 개수 또는 텐서의 차원
#1차원 tensor(vector)
d=np.array([1,2,3,4])
print(d.ndim,d.shape)
#vector에서 차원=원소 개수, 텐서에서의 차원=축의 개수
#2차원 tensor(행렬)
d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print("텐서의 차원:",d.ndim,'텐서의 크기:',d.shape)
#텐서의 크기(shape)=축을 따라서 얼마나 많은 차원이 있는지
#3차원 텐서(tensor)
d = np.array([
[[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [10, 11, 12, 13, 14]],
[[15, 16, 17, 18, 19], [19, 20, 21, 22, 23], [23, 24, 25, 26, 27]]
])
print('텐서의 차원:',d.ndim,'텐서의 크기:',d.shape)
- 3차원 텐서
시퀀스 데이터 표현할 때 자주 사용된다.(단어의 시퀀스 의미)
샘플의 개수=samples or batch_size
시퀀스의 길이=timesteps
단어를 표현하는 벡터의 차원=word_dim
왜 자연어 처리에서 3D텐서 개념이 사용되는지 예를 살표 보자
문서 1:I like NLP
문서 2:I like DL
문서 3:DL isAI
다음과 같은 훈련 데이터가 있다고 해보자
이를 인공 신경망의 모델의 입력으로 사용하기 위해서는 각 단어를 벡터화해야 한다.
원-핫 인코딩으로 각 단어를 벡터화해보자
I [1 0 0 0 0 0]
like [0 1 0 0 0 0]
NLP [0 0 1 0 0 0]
DL [0 0 0 1 0 0]
is [0 0 0 0 1 0]
AI [0 0 0 0 0 1]
위의 벡터들을 인공 신경망의 입력으로 한꺼번에 사용하고자 하면 다음과 같이 바꿀 수 있다
[[[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0]],
[[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0]],
[[0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 1]]]Batch=훈련데이터를 다수 묶어 입력으로 사용하는 것
-그 이상의 텐서

3. 벡터와 행렬의 연산
1) 벡터 행렬 덧셈 뺄셈
#벡터의 덧셈 뺄셈
import numpy as np
A=np.array([8,4,5])
B=np.array([1,2,3])
print(A+B,A-B)
#행렬의 덧셈 뺄셈
A = np.array([[10, 20, 30, 40], [50, 60, 70, 80]])
B = np.array([[5, 6, 7, 8],[1, 2, 3, 4]])
print(A+B, "\n",A-B)
2) 벡터 내적과 행렬 곱셈
- 벡터 내적
내적 성립 조건=두 벡터의 차원이 같다. 두 벡터 중 앞의 벡터가 행벡터. 뒤의 벡터가 열벡터이다.
내적의 결과는 스칼라이다

- 행렬내적
왼쪽 행렬의 행벡터와 오른쪽 행렬의 열벡터의 내적이 결과 행렬 원소가 된다.
행렬 곱셈의 조건
1. 두 행렬 곱이 J x K가 되려면 J의 열개수와 K의 행 개수는 같아야 한다.
2. J x K의 결과로 나온 행렬 JK의 크기는 J의 행렬 개수와 K의 열 개수를 가진다
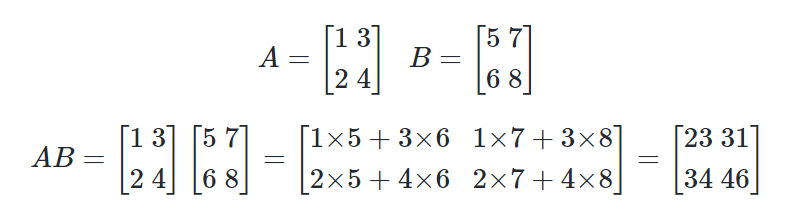
#벡터의 내적
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])
print('두 벡터의 내적 :',np.dot(A, B))
#행렬의 내적
A = np.array([[1, 3],[2, 4]])
B = np.array([[5, 7],[6, 8]])
print('두 행렬의 행렬곱 :')
print(np.matmul(A, B))
4. 다중 선형 회귀 행렬 연산으로 이해
독립 변수 2개 이상일 때 1개의 종속 변수 예측하는 문제를 행렬의 연산으로 표현해 보자
y=w1x1+w2x2+w3x3+...+wnxn+b

혹은

5. 샘플과 특성
[x1, x2, x3, x4,.. xn] --> sample1
x1--> feature1
x2--> feature2....
샘플=데이터를 셀 수 있는 단위로 구분할 때 각각을 부르는 이름
특성=y를 예측하기 위한 각각의 x
6. 가중치와 편향 행렬의 크기 결정
행렬 곱셈의 조건을 생각해 보자
1. 두 행렬 곱이 J x K가 되려면 J의 열개수와 K의 행 개수는 같아야 한다.
2. J x K의 결과로 나온 행렬 JK의 크기는 J의 행렬 개수와 K의 열 개수를 가진다
이 규칙을 사용해서
입력 출력 행렬 크기를 알면
W(가중치 행렬)와 B(편향 행렬)의 크기를 찾아낼 수 있다.
독립 변수 행렬을 X 종속 변수 행렬을 Y라고 할 때
행렬 X=input Matrix, 행렬 Y=Output Matrix라고 하자.
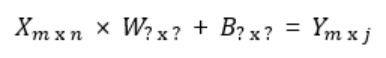
B와 Y의 행렬 크기는 같아야 한다.(그래야지 덧셈이 계산이 됨)
X행렬 열의 크기와 W행렬 행의 크기가 같아야 한다.(그래야지 XxW가 계산이 됨)
XxW의 결과인 Y행렬의 열 크기는 X행렬의 열크기와 같아야 한다.
결과적으로 아래와 같은 크기를 구할 수 있고 총 매개변수의 개수를 쉽게 계산할 수 있다.

'개발 > AI' 카테고리의 다른 글
| [Pytorch] 06. 인공 신경망 (1) | 2024.08.02 |
|---|---|
| [Pytorch] 05. 소프트맥스 회귀 (0) | 2024.07.30 |
| [Pytorch] 04. 로지스틱 회귀 (0) | 2024.07.30 |
| [OpenCV] 컴퓨터 비전과 딥러닝 / Ch03 / 연습 문제 (0) | 2024.07.08 |
| [OpenCV] 컴퓨터 비전과 딥러닝 / Ch02 / 연습 문제 (0) | 2024.07.03 |

